数式処理言語Maximaの紹介
INOUE Takakatsu 2020-09-28
言語エンジンeng_langの環境設定
source("eng_lang_setup.R")## === knitr, reticulate, eng_lang are go. ===数式処理言語Maxima
Maxima(マキシマ)は、LISP で記述された数式処理システムである。GNU GPL に基づくフリーソフトウェアであり、現在も活発に開発が続けられている。Maple や Mathematica などの商用の数式処理システムと比べても遜色のない機能を持っている。
[略史] Maxima の起源は、マサチューセッツ工科大学の MACプロジェクトによって開発され、米国エネルギー省によって配布されていた Macsyma の1982年のバージョンを GNU Common Lisp に移植したものである。 1982年から Macsyma の独自のバージョンを管理・維持していたビル・シェルター (en) が、1998年にエネルギー省から GPLライセンスを適用することを条件に公開の許可を得た。こうして公開されたプログラムは Maxima と呼ばれることになり、2001年のシェルターの死後も開発者や利用者のグループによって独自に開発が続けられている。(Wikipediaより引用)
Maximaのフロント・エンド
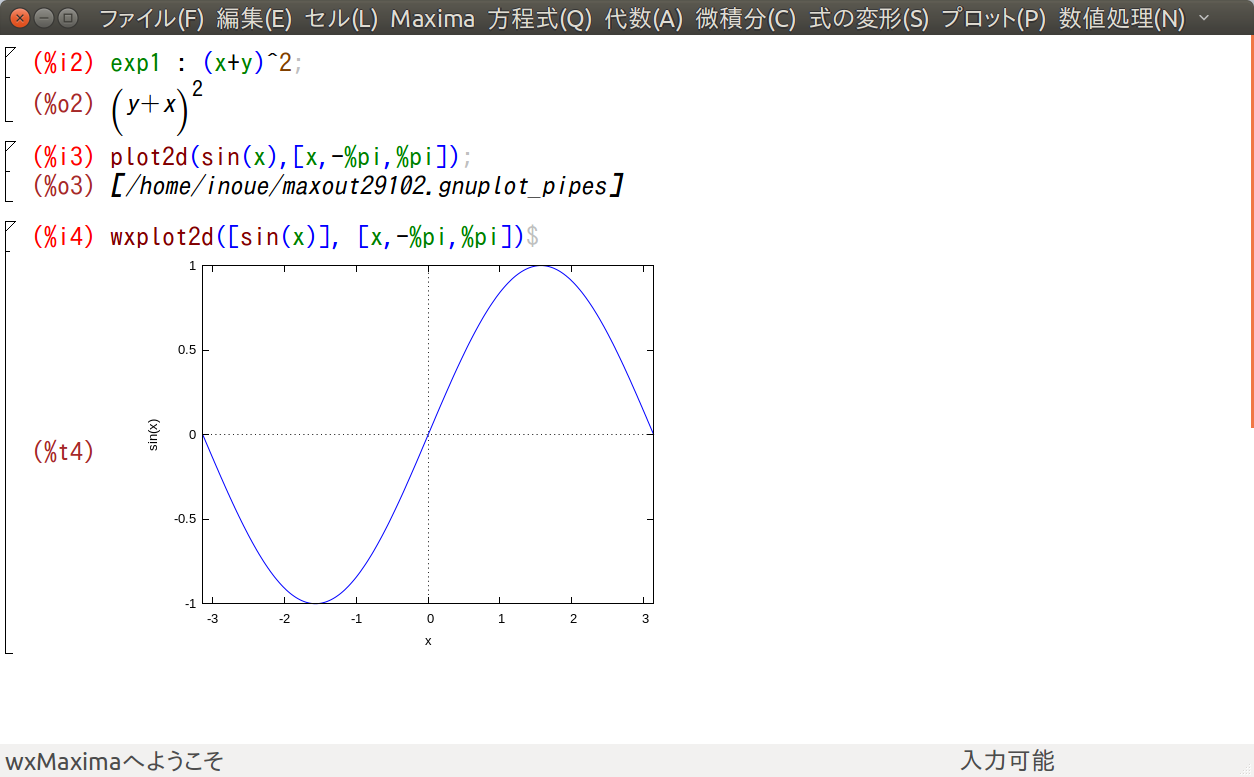
図1. fig-wxmax.png
数式処理機能:
準備: /*comment*/,行末:$,;(表示), system("ls"),load(mxinit)
定数:%pi, %i, %e, inf, minf, infinity, float(%pi), true, false
ヘルプ: apropos(exp), example(exp), describe(exp), ? exp
例: kill(all); f(x) := (x+a)^2; expand(f(x)); quit();
複素数: %i, realpart(z),imagpart(z),rectform(z),polarform(z)
abs(z),carg(z), rectform(poloarform(z))
微積: diff(f(x),x), diff(f(x),x,2), integrate(f(x),x,x0,x1)
展開: expand(f(x)), taylor(f(x),x,x0,power),trigexpand:true
因数分解:factor(f(x)), ratsimp(%), numer:true, radcan(exp)
総和: sum(i^2,i,1,3),nsum, 極限:limit(f(x),x,x0,plus)
作図: plot2d(f(x),[x,x0,x1]), system(\"~/bin/myplot2\");
方程式:solve(x^2-2*x-1=0,x), roots, nroots, ode2(eq,y[x],x)
solve([a*x+b*y=e,c*x+d*y=f],[x,y]) 不定方程式も可
行列:A : matrix([a11,a12],[a21,a22]), ident(3), A.B, invert(A)
transpose(A), determinant(A), rank(A), invert(A)
私用関数: on3lib(); mylib(MATLIB); myreset(); fundef(func); functions;
[詳細] ---> q(arg) : index, mat, macro, display
プログラム機能:
q | max : 全般(始めに) env : 環境 disp | display : 表示 funcs : 主な関数 rat : 有理式 simple : 式の簡約化 taylor : Taylor展開 solve : 方程式 complex : 複素数 trig : 三角関数 rule | let : 規則定義 string | str : 文字列操作 vect : ベクトル matrix | mat : 行列 macro | func : マクロ(関数) ifthen : 条件判定 fordo|loop : くり返し list : リスト graph | plot : 作図 draw : 作図2 tex | file : TeX出力 ask | typep : 型判定 call in MAXima by q(arg);
実行例1: 式の展開,因数分解,方程式の求解
echo '
(linel:70)$ /* 行長を指定(コメント例) */
exp1 : (x+y)^2; /* 式の定義 */
exp2 : expand(exp1); /* 式exp1を展開 */
(display2d:false)$ /* 表示形式の変更 */
factor(exp2); /* 式exp2を因数分解 */
solve(x^2-2*x-1=0,x); /* 2次方程式の求解 */
solve([a*x+b*y=e,c*x+d*y=f],[x,y]); /* 連立方程式の求解 */
' > /tmp/tmp.mx
maxima -b /tmp/tmp.mx##
## Maxima 5.43.2 http://maxima.sourceforge.net
## using Lisp GNU Common Lisp (GCL) GCL 2.6.12
## Distributed under the GNU Public License. See the file COPYING.
## Dedicated to the memory of William Schelter.
## The function bug_report() provides bug reporting information.
## (%i1) batch("/tmp/tmp.mx")
##
## read and interpret /tmp/tmp.mx
## (%i2) linel:70
## (%i3) exp1:(x+y)^2
## 2
## (%o3) (y + x)
## (%i4) exp2:expand(exp1)
## 2 2
## (%o4) y + 2 x y + x
## (%i5) display2d:false
## (%i6) factor(exp2)
## (%o6) (y+x)^2
## (%i7) solve(x^2-2*x-1 = 0,x)
## (%o7) [x = 1-sqrt(2),x = sqrt(2)+1]
## (%i8) solve([a*x+b*y = e,c*x+d*y = f],[x,y])
## (%o8) [[x = -(d*e-b*f)/(b*c-a*d),y = (c*e-a*f)/(b*c-a*d)]]
## (%o10) "/tmp/tmp.mx"
注0: (%i1) batch("/tmp/tmp.mx") と (%o9) "/tmp/tmp.mx" は無視して下さい.
注1: (%i1) は1番目の入力(input)行を表し, (%o3) は3番目の出力(output)行を表す.
注2: 行末が "$" のときは出力非表示を, ";" のとき出力表示を指示する.
注3: wxMaximaでは入力後に "SHIFT ENTER"を入力するとその行が実行される.
注4: PowerPointへの貼り付けは,wxmaximaで"編集→画像としてコピー”を選択する.
実行例2: 数学関数
echo '
(linel:70,display2d:false)$ /* 行長を指定(コメント例) */
sin(%pi/3); /* x=%pi/3=60° のときの正弦関数 sin(x) の値を求める */
asin(1/2); /* 逆正弦関数 sin^{-1}(1/2) の値を求める */
trigexpand(sin(a+b)); /* sin(a+b) を展開する */
exp(1); /* 自然対数の底 %e を表示する */
float(exp(1)); /* 自然対数の底 %e の数値表現を求める */
log(1); /* 自然対数 log_{e}(1) を求める */
log(%e); /* 自然対数 log_{e}(%e) を求める */
' > /tmp/tmp.mx
maxima -b /tmp/tmp.mx##
## Maxima 5.43.2 http://maxima.sourceforge.net
## using Lisp GNU Common Lisp (GCL) GCL 2.6.12
## Distributed under the GNU Public License. See the file COPYING.
## Dedicated to the memory of William Schelter.
## The function bug_report() provides bug reporting information.
## (%i1) batch("/tmp/tmp.mx")
##
## read and interpret /tmp/tmp.mx
## (%i2) (linel:70,display2d:false)
## (%i3) sin(%pi/3)
## (%o3) sqrt(3)/2
## (%i4) asin(1/2)
## (%o4) %pi/6
## (%i5) trigexpand(sin(a+b))
## (%o5) cos(a)*sin(b)+sin(a)*cos(b)
## (%i6) exp(1)
## (%o6) %e
## (%i7) float(exp(1))
## (%o7) 2.718281828459045
## (%i8) log(1)
## (%o8) 0
## (%i9) log(%e)
## (%o9) 1
## (%o11) "/tmp/tmp.mx"実行例3: 行列
echo '
(linel:70)$ /* 行長を指定(コメント例) */
A : matrix([a,b],[c,d]); /* (2x2)行列Aを定める */
invert(A); /* (2x2)行列Aの逆行列を求める */
determinant(A); /* (2x2)行列Aの行列式(determinant)の値を求める */
rank(A); /* (2x2)行列Aの階数(rank)を求める */
' > /tmp/tmp.mx
maxima -b /tmp/tmp.mx##
## Maxima 5.43.2 http://maxima.sourceforge.net
## using Lisp GNU Common Lisp (GCL) GCL 2.6.12
## Distributed under the GNU Public License. See the file COPYING.
## Dedicated to the memory of William Schelter.
## The function bug_report() provides bug reporting information.
## (%i1) batch("/tmp/tmp.mx")
##
## read and interpret /tmp/tmp.mx
## (%i2) linel:70
## (%i3) A:matrix([a,b],[c,d])
## [ a b ]
## (%o3) [ ]
## [ c d ]
## (%i4) invert(A)
## [ d b ]
## [ --------- - --------- ]
## [ a d - b c a d - b c ]
## (%o4) [ ]
## [ c a ]
## [ - --------- --------- ]
## [ a d - b c a d - b c ]
## (%i5) determinant(A)
## (%o5) a d - b c
## (%i6) rank(A)
## (%o6) 2
## (%o8) /tmp/tmp.mxテイラー展開とは
複雑な関数\(f(x)\)を変数\(x\)の多項式で近似する一つの手法として知られている.
テイラー展開
関数\(f(x)\)の点\(x_0\)における\(n\)次のテイラー展開(近似式)は次式で表せる. \[\begin{eqnarray*} f(x) &\doteq& \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!}\,(x-x_0)^k \\ &=& f(x_0) + f'(x_0)\,(x-x_0) + \frac{f''(x_0)}{2}\,(x-x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!}\,(x-x_0)^n \end{eqnarray*}\]
ここで,\(f^{(k)}(x_0)\) は関数 \(f(x)\) の\(k\)次の導関数 \(f^{(k)}(x)\) において, 変数\(x\)に値\(x_0\)を代入した導関数値(微分係数)を表す.
なお,\(x_0=0\) としたテイラー展開を特に「マクローリン展開」という. また,1次のテイラー展開式は,\((x,\,y)=(x_0,\,f(x_0))\) を通る接線の方程式 \(y = f(x_0) + f'(x_0)\,(x-x_0)\) と一致する.
多項式のテイラー展開
[視点]多項式\(f(x)\)をより次数の低い多項式で近似する問題から始めよう.\ \(f(x) = x^3 -10x^2+27x-18\)を点\(x=2\)において0次から3次のテイラー展開を求める.\ 結果をグラフにしてテイラー展開のイメージを理解する.
echo '
(display2d:false, linel:70)$
goptions:[[gnuplot_term,png],[gnuplot_out_file,"Max_intro_2019_files/tmp-0.png"]]$
for i:1 thru length(goptions) do set_plot_option(goptions[i])$
f : expand((x-1)*(x-3)*(x-6));
plot2d(f,[x,0,6.5],[y,-10,10],grid2d,[ylabel,"f(x)"], [title,"Graph of f(x)"])$
' > /tmp/tmp.mx
maxima -b /tmp/tmp.mx##
## Maxima 5.43.2 http://maxima.sourceforge.net
## using Lisp GNU Common Lisp (GCL) GCL 2.6.12
## Distributed under the GNU Public License. See the file COPYING.
## Dedicated to the memory of William Schelter.
## The function bug_report() provides bug reporting information.
## (%i1) batch("/tmp/tmp.mx")
##
## read and interpret /tmp/tmp.mx
## (%i2) (display2d:false,linel:70)
## (%i3) goptions:[[gnuplot_term,png],
## [gnuplot_out_file,"Max_intro_2019_files/tmp-0.png"]]
## (%i4) for i thru length(goptions) do set_plot_option(goptions[i])
## (%i5) f:expand((x-1)*(x-3)*(x-6))
## (%o5) x^3-10*x^2+27*x-18
## (%i6) plot2d(f,[x,0,6.5],[y,-10,10],grid2d,[ylabel,"f(x)"],
## [title,"Graph of f(x)"])
## plot2d: some values were clipped.
## (%o7) "/tmp/tmp.mx"
図2. Max_intro_2019_files/tmp-0.png
注: wxmaximaから実行する場合はplot2d()はwxplot2d()に置き換えて実行してください.
\[ \begin{array}{ll} f(x) = x^3 -10x^2+27x-18 &\rightarrow f(2) = 4 \cr f'(x) = 3x^2-20x+27 &\rightarrow f'(2)=3\cdot2^2-20\cdot2+27 = -1\cr f''(x) = 6x-20 &\rightarrow f''(2)=-8 \cr f^{(3)}(x) = 6 &\rightarrow f^{(3)}(2)=6 \end{array} \] よって,2次のテイラー展開式は次式で表せる. \[ \begin{array}{ll} f(x) &\doteq f(2) + f'(2)(x-2) + \frac{f''(2)}{2}\,(x-2)^2 \cr &= 4 + (-1)(x-2) + (-4)(x-2)^2 \end{array} \] 同様にして,3次のテイラー展開式は次式で表せる. \[ \begin{array}{ll} f(x) &\doteq f(2) + f'(2)(x-2) + \frac{f''(2)}{2}\,(x-2)^2 + \frac{f^{(3)}(2)}{3!}\,(x-2)^3 \cr &= 4 + (-1)(x-2) + (-4)(x-2)^2 + (x-2)^3 \cr &= x^3 - 10x^2 + 27x -18 \end{array} \]
echo '
(display2d:false, linel:70)$
goptions:[[gnuplot_term,png],[gnuplot_out_file,"Max_intro_2019_files/tmp-1.png"]]$
for i:1 thru length(goptions) do set_plot_option(goptions[i])$
f : expand((x-1)*(x-3)*(x-6));
t1 : taylor(f,x,2,1);
t2 : taylor(f,x,2,2);
plot2d([f,t1,t2],[x,0,6.5],[y,-10,10], grid2d)$
/* system("evince Max_intro_2019_files/tmp-1.eps")$ */
' > /tmp/tmp.mx
maxima -b /tmp/tmp.mx##
## Maxima 5.43.2 http://maxima.sourceforge.net
## using Lisp GNU Common Lisp (GCL) GCL 2.6.12
## Distributed under the GNU Public License. See the file COPYING.
## Dedicated to the memory of William Schelter.
## The function bug_report() provides bug reporting information.
## (%i1) batch("/tmp/tmp.mx")
##
## read and interpret /tmp/tmp.mx
## (%i2) (display2d:false,linel:70)
## (%i3) goptions:[[gnuplot_term,png],
## [gnuplot_out_file,"Max_intro_2019_files/tmp-1.png"]]
## (%i4) for i thru length(goptions) do set_plot_option(goptions[i])
## (%i5) f:expand((x-1)*(x-3)*(x-6))
## (%o5) x^3-10*x^2+27*x-18
## (%i6) t1:taylor(f,x,2,1)
## (%o6) 4-(x-2)
## (%i7) t2:taylor(f,x,2,2)
## (%o7) 4-(x-2)-4*(x-2)^2
## (%i8) plot2d([f,t1,t2],[x,0,6.5],[y,-10,10],grid2d)
## plot2d: some values were clipped.
## plot2d: some values were clipped.
## (%o10) "/tmp/tmp.mx"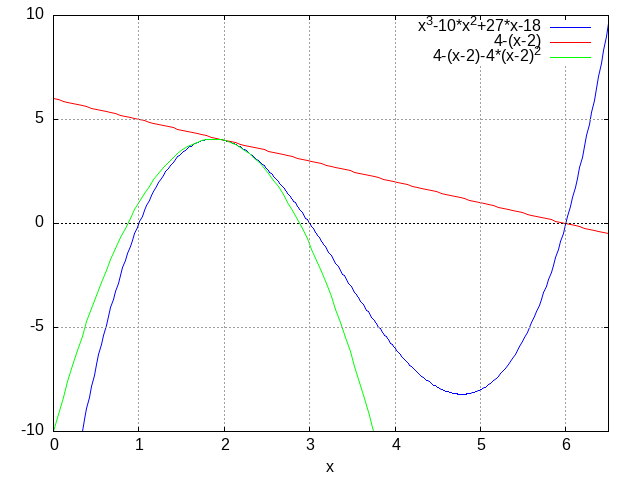
図3. Max_intro_2019_files/tmp-1.png
\(f(x)\)の点\(x=2\)における1次,2次のTaylor展開式のグラフ
##
## Maxima 5.43.2 http://maxima.sourceforge.net
## using Lisp GNU Common Lisp (GCL) GCL 2.6.12
## Distributed under the GNU Public License. See the file COPYING.
## Dedicated to the memory of William Schelter.
## The function bug_report() provides bug reporting information.
## (%i1) batch("/tmp/tmp.mx")
##
## read and interpret /tmp/tmp.mx
## (%i2) (load(draw),display2d:false,linel:70)
## (%i3) f:expand((x-1)*(x-3)*(x-6))
## (%i4) for i thru 3 do define(t[i](x,x0),taylor(f,x,x0,i))
## (%o4) done
## (%i5) g1:gr2d(xrange = [0,6.5],yrange = [-10,10],grid = true,
## font = "Arial",font_size = 24,title = "x0 = 2",
## color = red,key = "f(x)",explicit(f,x,0,6.5),
## color = blue,key = "f1(x)",explicit(t[1](x,2),x,0,6.5),
## color = green,key = "f2(x)",
## explicit(t[2](x,2),x,0,6.5))
## (%i6) g2:gr2d(xrange = [0,6.5],yrange = [-10,10],grid = true,
## title = "x0=3",color = red,key = "f(x)",
## explicit(f,x,0,6.5),color = blue,key = "f1(x)",
## explicit(t[1](x,3),x,0,6.5),color = green,
## key = "f2(x)",explicit(t[2](x,3),x,0,6.5))
## (%i7) draw(terminal = png,file_name = "Max_intro_2019_files/tmp-2",
## columns = 2,dimensions = [1000,400],g1,g2)
## (%o8) "/tmp/tmp.mx"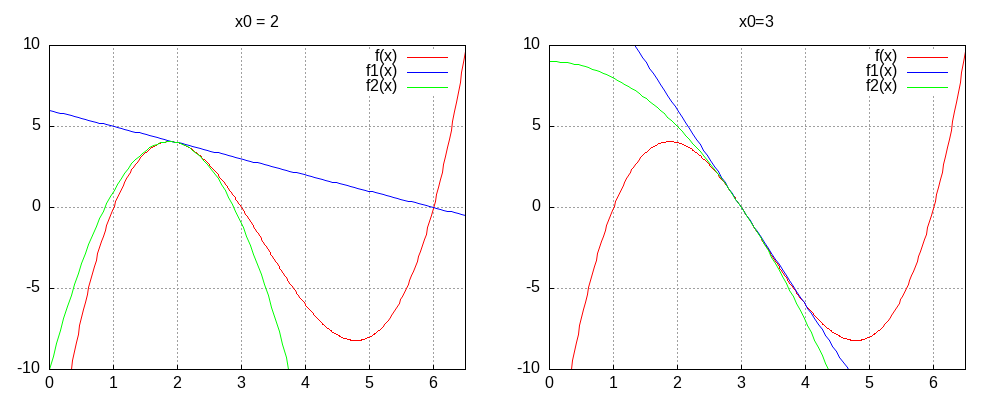
図4. Max_intro_2019_files/tmp-2.png
点\(x_0\)の変化(左図:\(x_0=2\),,右図:\(x_0=3\))とTaylor展開 \[ f(x) \doteq f(x_0) + f'(x_0)\,(x-x_0) + \frac{f''(x_0)}{2}\,(x-x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!}\,(x-x_0)^n \]
一般関数のテイラー展開
echo '
(load(draw), display2d:false, linel:70)$
f : sin(x)$
for i:1 thru 15 do ( define(t[i](x,x0), taylor(f,x,x0,i)) )$
x0 : 0$
g1 : gr2d(xrange = [-%pi,%pi], yrange = [-1.5, 1.5], grid=true,
font="Arial", font_size=24,
title="n=1,3,7",
color=black, key="f(x)", explicit(f, x, -%pi, %pi),
color=red,key="f1(x)",explicit(t[1](x,x0), x,-%pi,%pi),
color=green,key="f3(x)",explicit(t[3](x,x0),x,-%pi,%pi),
color=blue,key="f7(x)",explicit(t[7](x,x0),x,-%pi,%pi)
)$
draw(terminal=png, file_name="Max_intro_2019_files/tmp-3",columns=1, g1,
dimensions=[1500,900])$
' > /tmp/tmp.mx
maxima -b /tmp/tmp.mx##
## Maxima 5.43.2 http://maxima.sourceforge.net
## using Lisp GNU Common Lisp (GCL) GCL 2.6.12
## Distributed under the GNU Public License. See the file COPYING.
## Dedicated to the memory of William Schelter.
## The function bug_report() provides bug reporting information.
## (%i1) batch("/tmp/tmp.mx")
##
## read and interpret /tmp/tmp.mx
## (%i2) (load(draw),display2d:false,linel:70)
## (%i3) f:sin(x)
## (%i4) for i thru 15 do define(t[i](x,x0),taylor(f,x,x0,i))
## (%i5) x0:0
## (%i6) g1:gr2d(xrange = [-%pi,%pi],yrange = [-1.5,1.5],grid = true,
## font = "Arial",font_size = 24,title = "n=1,3,7",
## color = black,key = "f(x)",explicit(f,x,-%pi,%pi),
## color = red,key = "f1(x)",
## explicit(t[1](x,x0),x,-%pi,%pi),color = green,
## key = "f3(x)",explicit(t[3](x,x0),x,-%pi,%pi),
## color = blue,key = "f7(x)",
## explicit(t[7](x,x0),x,-%pi,%pi))
## (%i7) draw(terminal = png,file_name = "Max_intro_2019_files/tmp-3",
## columns = 1,g1,dimensions = [1500,900])
## (%o8) "/tmp/tmp.mx"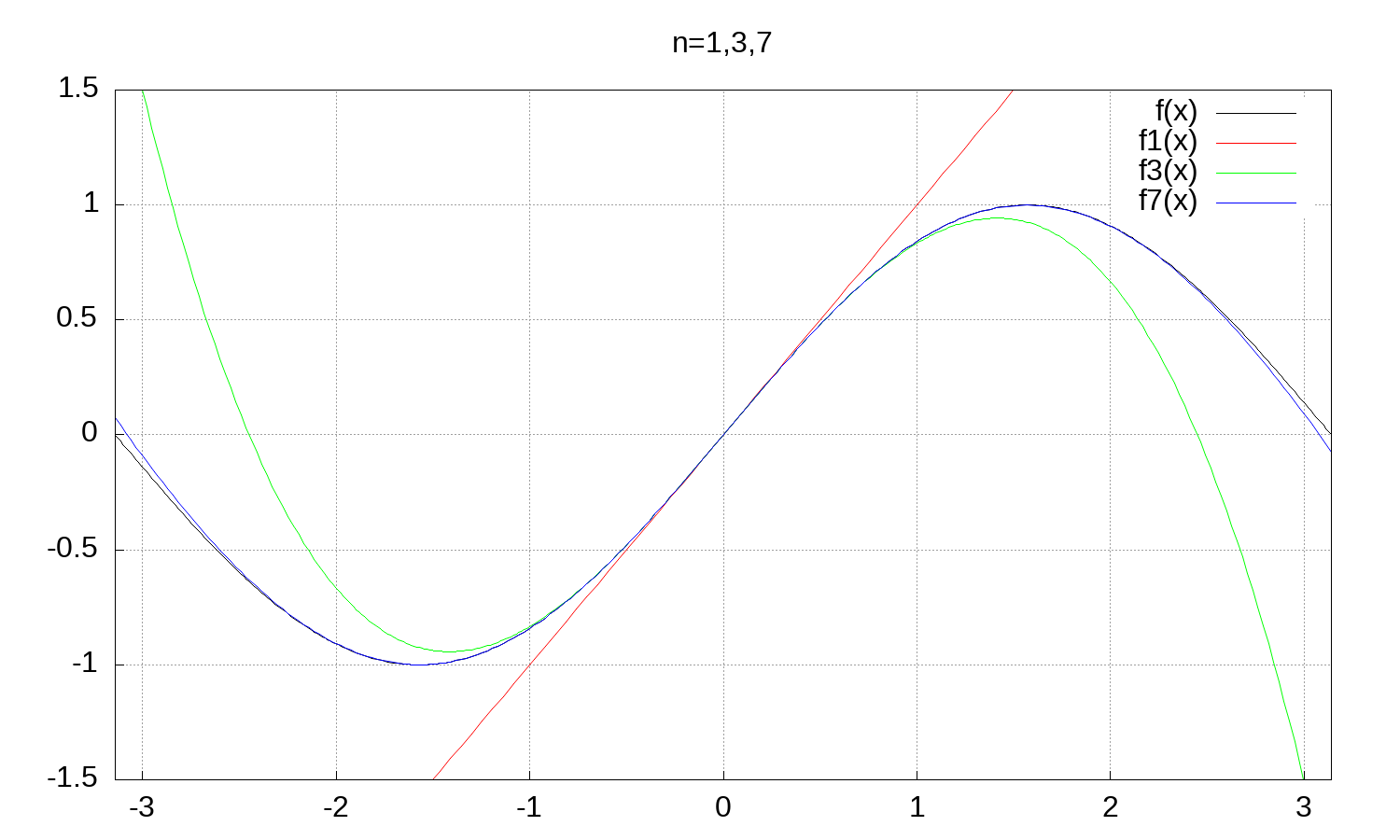
図5. Max_intro_2019_files/tmp/tmp-3.png
次数\(n\)の変化とTaylor展開(\(x_0=0)\)